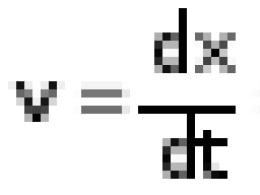Различные преобразования выражений содержащих степень. Степенные выражения (выражения со степенями) и их преобразование
Муниципальное казённое общеобразовательное учреждение
основная общеобразовательная школа № 25
Урок алгебры
Тема:
« Преобразование выражений, содержащих степени с дробными показателями»
Разработала:
,
учитель математики
высшей к валификационной категории
Узловая
2013
Тема урока : Преобразование выражений, содержащих степени с дробными показателями
Цель урока :
1. Дальнейшее формирование умений, знаний, навыков преобразования выражений, содержащих степени с дробными показателями
2. Развитие умения находить ошибки, развитие мышления, творчества, речи, вычислительных навыков
3. Воспитание самостоятельности, интереса к предмету, внимательности, аккуратности.
ТСО: магнитная доска, контрольные карточки, таблицы, индивидуальные карточки, у школьников на столе чистые подписанные листы для индивидуальной работы, кроссворд, таблицы для математической разминки, мультимедийный проектор.
Тип урока : закрепление ЗУН.
План урока во времени
1. Организационные моменты (2 мин)
2. Проверка домашнего задания (5 мин)
3. Разгадывание кроссворда (3 мин)
4. Математическая разминка (5 мин)
5. Решение упражнений на закрепление фронтально (7 мин)
6. Индивидуальные работы (10 мин)
7. Решение упражнений на повторение (5 мин)
8. Итог урока (2 мин)
9. Задание на дом (1 мин)
Ход урока
1) Проверка домашнего задания в форме взаимопроверки . Хорошие ученики проверяют тетради у слабых ребят. А слабые ребята проверяют у сильных по образцу контрольной карточки. Домашнее задание дано в двух вариантах.
I вариант задание нетрудное
II вариант задание сложное
В результате проверки ребята подчёркивают ошибки простым карандашом и ставят оценку. Окончательно я проверяю работы, после того, как ребята сдадут тетради после урока. Я спрашиваю у ребят результаты их проверки и выставляю оценки за этот вид работы в свою таблицу подведения итогов.
2) Для проверки теоретического материала предлагается кроссворд .
По вертикали:
1. Свойство умножения, используемое при умножении одночлена на многочлен?
2. Действие показателей степени при возведении степени в степень?
3. Степень с нулевым показателем?
4. Произведение, состоящее из одинаковых множителей?
По горизонтали:
5. Корень n – ой степени из неотрицательного числа?
6. Действие показателей при умножении степеней?
7. Действие показателей степени при делении степеней?
8. Число всех одинаковых множителей?
3) Математическая разминка
а) выполните вычисление и с помощью шифра прочтите запрятанное в задачу слово.
На доске перед вами таблица. В таблице в графе 1 записаны примеры, которые надо вычислить.
Ключ к таблице
491/2 | ||
27-1/3 | ||
4*81/3 | ||
5*25-1/2 | ||
7*82/3 | ||
(49/144)1/2 | 7/12 | |
(27*64)1/3 |
7/12 |
А ответ записать в графе II , а в графе III поставить букву, соответствующую этому ответу.
Учитель: Итак, зашифрованное слово «степень». В следующем задании мы работаем со 2-й и 3-ей степенью
б) Игра «Смотри не ошибись»
Вместо точек поставьте число
а) х=(х…)2; б) а3/2 = (а1/2)…; в) а=(а1/3)…; г) 5… = (51/4)2; д) 34/3=(34/9)…; е) 74/5 = (7…)2; ж) х1/2=(х…)2; з) у1/2=(у…)2
Найдём ошибку:
А1/4 – 2а1/2 + 1 = (а1/
Итак, ребята, что же нужно было применить, для выполнения этого задания:
Свойство степеней: при возведении степени в степень показатели перемножаются;
4) А теперь приступаем к фронтальной письменной работе , используя результаты предыдущей работы. Открывают тетради записывают число, тему урока.
№ 000
а) а – в = (а1/2)2 – (в1/2)2 = (а1/2 – в1/2)*(а1/2 + в1/2)
б) а – в = (а1/3)3 – (в1/3)3 = (а1/3 – в1/3)*(а2/3 + а1/3 в1/3 + в2/3)
№ 000 (а, в, г, д)
а) m2 – 5 = m2 – (m1/2)2 = (m – 51/2)*(m+51/2)
в) a3 – 4 = (a3/2)2 – 22 = (a3/2 – 2)*(a3/2 +2)
г) x2/5 – y4/5 = (x1/5)2 – (y2/5)2 = (x1/5 – y2/5)*(x1/5 + y2/5)
д) 4 – a = 22 – (a1/2)2 = (2 – a1/2)*(2+a1/2)
№ 000 (а, г, е)
а) x3 – 2 = x3 – (21/3)3 = (x – 21/3)*(x2 + 21/3 x + 22/3)
г) a6/5 + 27 = (a2/5)3 + 33 = (a2/5 + 3)*(a4/3 – 3 a2/5 + 9)
е) 4 + y = (41/3)3 + (y1/3)3 = (41/3 + y1/3)*(42/3 + 41/3 y1/3 + y2/3)
Оценка
5) Работа по индивидуальным карточкам по четырём вариантам на отдельных листах
Задания с различной степенью сложности, выполняются без какой-либо подсказки учителя.
Проверяю работы сразу и ставлю оценки в свою таблицу и на листиках у ребят.
№ 000 (а, в, д, з)
а) 4*31/2/(31/2 – 3) = 4*31/2 /31/2*(1 – 31/2) = 4 / (1 – 31/2)
в) х + х1/2 /2х = х1/2*(х1/2+1)/ 2*(х1/2)2 = (х1/2+1)/ 2х1/2
д) (а2/3 – в2/3)/(а1/3 +в1/3) = (а1/3)2 – (в1/3)2/(а1/3 +в1/3) = (а1/3 + в1/3)*(а1/3 –в1/3)/(а1/3 + в1/3) = а1/3 – в1/3
з) (х2/3 - х1/3 у1/3 +у2/3)/(х +у) = ((х1/3)2 – х1/3 у1/3 + (у1/3)2)/((х1/3)3 +(у1/3)3) = ((х1/3)2 – х1/3 у1/3 +(у1/3)2)/(х1/3 +у1/3)*((х1/3)2 – х1/3 у1/3 + (у1/3)2) = 1/ (х1/3 +у1/3)
7) Работа по индивидуальным карточкам с различной степенью сложности . В некоторых упражнениях есть рекомендации учителя, так как материал усложнён и слабым ребятам трудно справляться с работой
Так же предлагается четыре варианта. Оценивание происходит сразу. Я заношу все оценки в таблицу.
Задача № из сборника
Учитель задаёт вопросы:
1. Что надо найти в задаче?
2. Что для этого нужно знать?
3. Как выразить время 1 пешехода и 2 пешехода?
4. Сравнить время 1 и 2 пешехода по условию задачи и составить уравнение.
Решение задачи:
Пусть х (км/ч) – скорость 1 пешехода
Х +1 (км/ч) – скорость 2 пешехода
4/х (ч) – время пешехода
4/(х +1) (ч) – время второго пешехода
По условию задачи 4/х >4/ (х +1) на 12 мин
12 мин = 12 /60 ч = 1/5 ч
Составляем уравнение
Х/4 – 4/ (х +1) = 1/5
НОЗ: 5х(х +1) ≠ 0
5*4*(х+1) – 5*4х = х*(х+1)
20х + 20 – 20х – х2 – х = 0
Х2 +х –20 = 0
Д=1 – 4*(-20) = 81, 81>0, 2 к
х1 = (-1 -√81)/(-2) = 5 км/ч – скорость 1 пешехода
х2 = (-1 + √81)/(-2) = 4 – не подходит по смыслу задачи, так как х>0
Ответ: 5 км/ч – скорость 2 пешехода
9) Итог урока : Итак, ребята, сегодня на уроке мы закрепили знания, умения, навыки преобразования выражений, содержащих степени, применяли формулы сокращённого умножения, вынос общего множителя за скобки, повторили пройденный материал. Указываю на достоинства и недостатки.
Подведение итогов урока в таблице.
Кроссворд | Мат. разминка | Фронт. работа | Инд. работа К-1 | Инд. работа К-2 | ||||
10)Объявляю оценки. Задание на дом
Индивидуальные карточки К – 1 и К – 2
Меняю В – 1 и В – 2 ; В – 3 и В – 4, так как они равносильные
Приложения к уроку.
1) Карточки для домашнего задания
1. упростите
а) (х1/2 – у1/2)2 + 2х1/2 у1/2
б) (а3/2 + 5а1\2)2 – 10а2
2. представьте в виде суммы
а) а1/3 с1\4*(в2/3 + с3/4)
б) (а1/2 – в1/2)*(а + а1/2 в1\2 + в)
3. вынесите общий множитель
в) 151/3 +201/3
1. упростите
а) √m + √n – (m1/4 – n1/4)2
б) (а1/4 +в1/4)*(а1/8 + в1/8)*(а1\8 – в1/8)
2. представьте в виде суммы
а) х0,5 у0,5*(х-0,5 – у1,5)
б) (х1/3 +у1/3)*(х2\3 – х1/3 у1\3 +у2/3)
3. Вынесите общий множитель за скобки
б) в1\3 – в
в) (2а)1/3 – (5а)1\3
2) контрольная карточка для В – 2
а) √m + √n – (m 1|4 – n 1|4)2 = m 1|2 + n 1|2 – ((m 1|2)2 – 2 m 1/4 n 1/4 + (n 1/2)2) = m 1/2 + n 1/2 – m 1/2 + 2 m 1/4 n 1/4 – n 1/2 = 2 m 1/4 n 1/4
б) (а1/4 + в1/4)*(а1/8 + в1/8)*(а1/8 – в1/8) = (а1/4 + в1/4)*(а1/8)2 – (в1/8)2 = (а1/4 + в1/4)*(а1/4 – в1/4) = (а1/4)2 – (в1/4)2 = а1/2 – в1/2
а) х0,5 у0,5* (х-0,5- у1,5) = х0,5 у0,5 х-0,5 – х0,5 у0,5у1,5 = х0 у0,5 – х0,5 у2 = у0,5 – х0,5 у2
б) (х1/3 + у1/3)*(х2/3 – х1/3 у1\3 + у2/3) = (х1\3 + у1/3)*((х1/3)2 – х1/3 у1\3 + (у1/3)2) = (х1/3)2 + (у1/3)2 = х +у
а) 3 – 31/2 = 31/2 * (31/2 - 1)
б) в1/3 – в = в1/3 *(1 – в2/3)
в) (2а)1/3 – (5а)1/3 = а1/3*(21/3 – 51/3)
3) Карточки для первой индивидуальной работы
а) а – у, х ≥ 0, у ≥ 0
б) а – и, а ≥ 0
1. Разложите на множители представив в виде разности квадратов
а) а1/2 – в1/2
2. Разложите на множители представив в виде разности или суммы кубов
а) c1/3 + d1/3
1. Разложите на множители представив в виде разности квадратов
а) Х1/2 + У1/2
б) Х1/4 – У1/4
2. Разложите на множители представив в виде разности или суммы кубов
4) карточки для второй индивидуальной работы
а) (х – х1/2)/ (х1/2 – 1)
Указание: х1/2 вынести за скобку числители
б) (а - в)/(а1/2 – в1/2)
Указание: а – в = (а1/2)2 – (в1/2)2
Сократите дробь
а) (21/4 – 2)/ 5*21/4
Указание: 21/4 вынести за скобку
б) (а – в)/(5а1/2 – 5в1/2)
Указание: а – в = (а1/2)2– (в1/2)2
Вариант 3
1. Сократите дробь
а) (х1/2 – х1/4)/х3/4
Указание: х1/4 вынести за скобку
б) (а1/2 – в1/2)/(4а1/4 – 4в1/4)
Вариант 4
Сократите дробь
а) 10/ (10 – 101/2)
б) (а - в)/(а2/3 + а1\3в1/3+ В 1/3)
Тема: «Преобразование выражений, содержащих степени с дробным показателем»
“Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь”. (М.В.Ломоносов)
Цели урока:
образовательные: обобщить и систематизировать знания учащихся по теме “Степень с рациональным показателем”;проконтролировать уровень усвоения материала;ликвидировать пробелы в знаниях и умениях учащихся;
развивающие: формировать навыки самоконтроля учащихся;создать атмосферу заинтересованности каждого ученика в работе, развивать познавательную активность учащихся;
воспитательные: воспитывать интерес к предмету, к истории математики.
Тип урока: урок обобщения и систематизации знаний
Оборудование: оценочные листы, карточки с заданиями, дешифраторами, кроссвордами для каждого учащегося.
Предварительная подготовка: класс разбит на группы, в каждой группе руководитель - консультант.
ХОД УРОКА
I. Организационный момент.
Учитель: Мы закончили изучение темы “Степень с рациональным показателем и её свойства”. Ваша задача на этом уроке, показать, как вы усвоили изученный материал и как вы умеете применять полученные знания при решении конкретных задач. На столе у каждого из вас есть оценочный лист. В него вы будете вносить свою оценку за каждый этап урока. В конце урока вы выставите средний балл за урок.
Оценочный лист
| Кроссворд | Разминка | Работа в | Уравнения | Проверь себя (с\р) | ||
II. Проверка домашней работы.
Взаимопроверка с карандашом в руках, ответы зачитываются учащимися.
III . Актуализация знаний учащихся.
Учитель: Известный французский писатель Анатоль Франс сказал в свое время: “Учиться надо весело.…Чтобы поглощать знания надо поглощать их с аппетитом”.
Повторим необходимые теоретические сведения в ходе разгадывания кроссворда.
По горизонтали:
1. Действие, с помощью которого вычисляется значение степени (возведение).
2. Произведение, состоящее из одинаковых множителей (степень).
3. Действие показателей степеней при возведении степени в степень (произведение).
4. Действие степеней, при которых показатели степеней вычитаются (деление).
По вертикали:
5. Число всех одинаковых множителей (показатель).
6. Степень с нулевым показателем (единица).
7. Повторяющийся множитель (основание).
8. Значение 10 5: (2 3 5 5) (четыре).
9. Показатель степени, который обычно не пишут (единица).
IV . Математическая разминка.
Учитель. Повторим определение степени с рациональным показателем и его свойства, выполним следующие задания.
1. Представить выражение х 22 в виде произведения двух степеней с основанием х, если один из множителей равен: х 2 , х 5,5 , х 1\3 , х 17,5 , х 0
2. Упростить:
б) у 5\8 у 1\4: у 1\8 = у
в) с 1,4 с -0,3 с 2,9
3. Вычислить и составить слово, используя дешифратор.
Выполнив это задание, вы, ребята, узнаете фамилию немецкого математика, который ввел термин - “показатель степени”.
1) (-8) 1\3 2) 81 1\2 3) (3\5) -1 4) (5\7) 0 5) 27 -1\3 6) (2\3) -2 7) 16 1\2 * 125 1\3
Слово: 1234567 (Штифель)
V. Письменная работа в тетрадях (ответы открываются на доске).
Задания:
1. Упростить выражение:
(х-2): (х 1\2 -2 1\2) (у-3): (у 1\2 – 3 1\2) (х-1): (х 2\3 -х 1\3 +1)
2. Найти значение выражения:
(х 3\8 х 1\4:) 4 при х=81
VI . Работа в группах.
Задание. Решить уравнения и составить слово, используя дешифратор.
Карточка № 1
Слово: 1234567 (Диофант)
Карточка № 2
Карточка № 3
Cлово: 123451 (Ньютон)
Дешифратор
Учитель. Все эти ученые внесли свой вклад в развитие понятия “степень”.
VII . Исторические сведения о развитии понятия степени (сообщение учащегося).
Понятие степени с натуральным показателем сформировалось ещё у древних народов. Квадрат и куб числа использовались для вычисления площадей и объемов. Степени некоторых чисел использовались при решении отдельных задач учеными Древнего Египта и Вавилона.
В III веке вышла книга греческого ученого Диофанта “Арифметика”, в которой было положено начало введению буквенной символики. Диофант вводит символы для первых шести степеней неизвестного и обратных им величин. В этой книге квадрат обозначается знаком с индексом r; куб – знаком k c индексом r и т.д.
Из практики решения более сложных алгебраических задач и оперирования со степенями возникла необходимость обобщения понятия степени и расширения его посредством введения в качестве показателя нуля, отрицательных и дробных чисел. К идее обобщения понятия степени на степень с ненатуральным показателем математики пришли постепенно.
Дробные показатели степени и наиболее простые правила действии над степенями с дробными показателями встречаются у французского математика Николая Орема (1323–1382 гг.) в его труде “Алгоритм пропорций”.
Равенство, а 0 =1 (для а не равного 0) применял в своих трудах в начале ХV века самаркандский ученый Гиясаддин Каши Джемшид. Независимо от него нулевой показатель был введен Николаем Шюке в ХV веке. Известно, что Николай Шюке (1445–1500 гг.), рассматривал степени с отрицательными и нулевым показателями.
Позже дробные и отрицательные, показатели встречаются в “Полной арифметике” (1544 г.) немецкого математика М.Штифеля и у Симона Стевина. Симон Стевин предположил подразумевать под а 1/n корень .
Немецкий математик М.Штифель (1487–1567 гг.) дал определение а 0 =1 при и ввел название показатель (это буквенный перевод с немецкого Exponent). Немецкое potenzieren означает возведение в степень.
В конце ХVI века Франсуа Виет ввел буквы для обозначения не только переменных, но и их коэффициентов. Он применял сокращения: N, Q, C – для первой, второй и третьей степеней. Но современные обозначения (типа а 4 , а 5) в XVII ввел Рене Декарт.
Современные определения и обозначения степени с нулевым, отрицательным и дробным показателем берут начало от работ английских математиков Джона Валлиса (1616–1703) и Исаака Ньютона (1643–1727).
О целесообразности введения нулевого, отрицательных и дробных показателей и современных символов впервые подробно писал в 1665 г. английский математик Джон Валлис. Его дело завершил Исаак Ньютон, который стал систематически применять новые символы, после чего они вошли в общий обиход.
Введение степени с рациональным показателем является одним из многих примеров обобщение понятий математического действия. Степень с нулевым, отрицательным и дробными показателями определяется таким образом, чтобы к ней были применены те же правила действий, которые имеют место для степени с натуральным показателем, т.е. чтобы сохранились основные свойства первоначального определённого понятия степени.
Новое определение степени с рациональным показателем не противоречит старому определению степени с натуральным показателем, то есть смысл нового определения степени с рациональным показателем сохраняется и для частного случая степени с натуральным показателем. Этот принцип, соблюдаемый при обобщении математических понятий, называется принципом перманентности (сохранения постоянства). В несовершенной форме его высказал 1830 г. английский математик Дж.Пикок, полностью и четко его установил немецкий математик Г.Ганкель в 1867 г.
VIII . Проверь себя.
Самостоятельная работа по карточкам (ответы открываются на доске).
Вариант 1
1. Вычислить: (1 балл)
(а + 3а 1\2): (а 1\2 +3)
Вариант 2
1. Вычислить: (1 балл)
2. Упростить выражение: по 1 баллу
а) х 1,6 х 0,4 б)(х 3\8) -5\6
3. Решить уравнение: (2 балла)
4. Упростить выражение: (2 балла)
5. Найти значение выражения: (3 балла)
IX . Подведение итогов урока.
Какие формулы и правила вспомнили на уроке?
Проанализируйте свою работу на уроке.
Оценивается работа учащихся на уроке.
Х. Домашнее задание. К: Р IV (повторить) ст.156-157 № 4 (а-в), № 7 (а-в),
Дополнительно: № 16
Приложение
Оценочный лист
Ф/И/ учащегося__________________________________________
| Кроссворд | Разминка | Работа в | Уравнения | Проверь себя (с\р) | ||
Карточка № 1
1) Х 1\3 =4; 2) у -1 =3\5; 3) а 1\2 = 2\3; 4) х -0,5 х 1,5 = 1; 5) у 1\3 =2; 6) а 2\7 а 12\7 = 25; 7) а 1\2: а = 1\3
Дешифратор
Карточка № 2
1) Х 1\3 =4; 2) у -1 = 3; 3) (х+6) 1\2 = 3; 4) у 1\3 =2; 5) (у-3) 1\3 =2; 6) а 1\2: а = 1\3
Дешифратор
Карточка № 3
1) а 2\7 а 12\7 = 25; 2) (х-12) 1\3 =2; 3) х -0,7 х 3,7 = 8; 4) а 1\2: а = 1\3; 5) а 1\2 = 2\3
Дешифратор
Карточка № 1
1) Х 1\3 =4; 2) у -1 =3\5; 3) а 1\2 = 2\3; 4) х -0,5 х 1,5 = 1; 5) у 1\3 =2; 6) а 2\7 а 12\7 = 25; 7) а 1\2: а = 1\3
Дешифратор
Карточка № 2
1) Х 1\3 =4; 2) у -1 = 3; 3) (х+6) 1\2 = 3; 4) у 1\3 =2; 5) (у-3) 1\3 =2; 6) а 1\2: а = 1\3
Дешифратор
Карточка № 3
1) а 2\7 а 12\7 = 25; 2) (х-12) 1\3 =2; 3) х -0,7 х 3,7 = 8; 4) а 1\2: а = 1\3; 5) а 1\2 = 2\3
Дешифратор
Карточка № 1
1) Х 1\3 =4; 2) у -1 =3\5; 3) а 1\2 = 2\3; 4) х -0,5 х 1,5 = 1; 5) у 1\3 =2; 6) а 2\7 а 12\7 = 25; 7) а 1\2: а = 1\3
Дешифратор
Карточка № 2
1) Х 1\3 =4; 2) у -1 = 3; 3) (х+6) 1\2 = 3; 4) у 1\3 =2; 5) (у-3) 1\3 =2; 6) а 1\2: а = 1\3
Дешифратор
Карточка № 3
1) а 2\7 а 12\7 = 25; 2) (х-12) 1\3 =2; 3) х -0,7 х 3,7 = 8; 4) а 1\2: а = 1\3; 5) а 1\2 = 2\3
Дешифратор
| Вариант 1 1. Вычислить: (1 балл) 2. Упростить выражение: по 1 баллу а) х 1\2 х 3\4 б)(х -5\6) -2\3 в) х -1\3: х 3\4 г) (0,04х 7\8) -1\2 3. Решить уравнение: (2 балла) 4. Упростить выражение: (2 балла) (а + 3а 1\2): (а 1\2 +3) 5. Найти значение выражения: (3 балла) (У 1\2 -2) -1 - (У 1\2 +2) -1 при у=18 | Вариант 2 1. Вычислить: (1 балл) 2. Упростить выражение: по 1 баллу а) х 1,6 х 0,4 б)(х 3\8) -5\6 в) х 3\7: х -2\3 г) (0,008х -6\7) -1\3 3. Решить уравнение: (2 балла) 4. Упростить выражение: (2 балла) (в 1,5 с- вс 1,5): (в 0,5 - с 0,5) 5. Найти значение выражения: (3 балла) (х 3\2 +х 1\2): (х 3\2 -х 1\2) при х=0,75 |
|||||||||||||
Разделы: Математика
Класс: 9
ЦЕЛЬ: Закрепить и усовершенствовать навыки применения свойств степени с рациональным показателем; развивать навыки выполнения простейших преобразований выражений, содержащих степени с дробным показателем.
ТИП УРОКА: урок закрепления и применения знаний по данной теме.
УЧЕБНИК: Алгебра 9 под ред. С.А. Теляковского.
ХОД УРОКА
Вступительное слово учителя
“Люди, незнакомые с алгеброй, не могут представить себе тех удивительных вещей, которых можно достигнуть... при помощи названной науки”. Г.В. Лейбниц
Алгебра открывает перед нами двери в лабораторный комплекс “Степень с рациональным показателем”.
1. Фронтальный опрос
1) Дайте определение степени с дробным показателем.
2) Для какого дробного показателя определена степень с основанием равным нулю?
3) Определится ли степень с дробным показателем для отрицательного основания?
Задание: Представьте число 64 в виде степени с основанием - 2; 2; 8.
Куб какого числа равен 64?
Существует ли еще какой-нибудь способ представления числа 64 в виде степени с рациональным показателем?
2. Работа по группам
1 группа. Докажите, что выражения (-2) 3/4 ; 0 -2 не имеют смысла.
2 группа. Представьте степень с дробным показателем в виде корня: 2 2/3 ; 3 -1|3 ; -в 1,5 ; 5а 1/2 ; (x-y) 2/3 .
3 группа. Представьте в виде степени с дробным показателем: v3; 8 vа 4 ; 3v2 -2 ; v(x+y) 2/3 ; вvв.
3. Перейдем в лабораторию “Действие над степенями”
Частые гости лаборатории - астрономы. Они приносят свои “астрономические числа”, подвергают их алгебраической обработке и получают полезные результаты
Например, расстояние от Земли до туманности Андромеды выражается числом
95000000000000000000 = 95 10 18 км;
оно называется квинтиллион.
Масса солнца в граммах выражается числом 1983 10 30 гр - нональон.
Кроме этого, в лабораторию попадают и другие серьезные задачи. Например, часто возникает проблема вычисления выражений вида:
а) ; б) ; в) .
Сотрудники лаборатории производят такие вычисления наиболее удобным способом.
Вы можете подключиться к работе. Для этого повторим свойства степеней с рациональными показателями:
А теперь вычислите или упростите выражение, применяя свойства степеней с рациональными показателями:
1 группа:
2 группа:
3 группа:
Проверка: по одному человеку от группы у доски.
4. Задание на сравнение
Как, применяя свойства степеней, сравнить выражения 2 100 и 10 30 ?
Ответ:
2 100 =(2 10) 10 =1024 10 .
10 30 =(10 3) 10 =1000 10
1024 10 >1000 10
2 100 >10 30
5. А сейчас я приглашаю вас в лабораторию “Исследование степеней”.
Какие преобразования мы можем выполнять над степенями?
1) Представьте число 3 в виде степени с показателем 2; 3; -1.
2) Каким способом можно разложить на множители выражения а-в; в+в 1/2 ; а-2а 1/2 ; 2-х 2 ?
3) Сократите дробь с последующей взаимопроверкой:
4) Объясните выполненные преобразования и найдите значение выражения:

6. Работа с учебником. № 611(г, д, е).
1 группа: (г).
2 группа: (д).
3 группа: (е).
№ 629 (а, б).
Взаимопроверка.
7. Выполняем практикум (самостоятельная работа).
Даны выражения:

При сокращении каких дробей применяются формулы сокращенного умножения и вынесение за скобки общего множителя?
1 группа: № 1, 2, 3.
2 группа: № 4, 5, 6.
3 группа: № 7, 8, 9.
При выполнении задания можно пользоваться рекомендациями.
- Если в записи примера есть как степени с рациональным показателем, так и корни n-й степени, то запишите корни n-й степени в виде степеней с рациональным показателем.
- Постарайтесь упростить выражение, над которым выполняются действия: раскрытие скобок, применение формулы сокращенного умножения, переход от степени с отрицательным показателем к выражению, содержащему степени с положительным показателем.
- Определите порядок выполнения действий.
- Выполните действия, соблюдая порядок их выполнения.
Оценивает учитель, собрав тетради.
8. Домашнее задание: № 624, 623.
Выражением вида a (m/n) , где n - некоторое натуральное число, m - некоторое целое число и основание степени а больше нуля, называется степень с дробным показателем. Причем верным является следующее равенство. n√(a m) = a (m/n) .
Как мы уже знаем, числа вида m/n, где n - некоторое натуральное число, а m - некоторое целое число, называют дробными или рациональными числами. Из всего вышесказанного получаем, что степень определена, для любого рационального показателя степени и любого положительного основания степени.
Для любых рациональных чисел p,q и любых a>0 и b>0 верны следующие равенства:
- 1. (a p)*(a q) = a (p+q)
- 2. (a p):(b q) = a (p-q)
- 3. (a p) q = a (p*q)
- 4. (a*b) p = (a p)*(b p)
- 5. (a/b) p = (a p)/(b p)
Данные свойства широко используются при преобразовании различных выражений, где содержатся степени с дробными показателями.
Примеры преобразований выражений, содержащих степень с дробным показателем
Рассмотрим несколько примеров, демонстрирующих применение этих свойств для преобразования выражений.
1. Вычислить 7 (1/4) * 7 (3/4) .
- 7 (1/4) * 7 (3/4) = z (1/4 + 3/4) = 7.
2. Вычислить 9 (2/3) : 9 (1/6) .
- 9 (2/3) : 9 (1/6) = 9 (2/3 - 1/6) = 9 (1/2) = √9 = 3.
3. Вычислить (16 (1/3)) (9/4) .
- (16 (1/3)) (9/4) = 16 ((1/3)*(9/4)) =16 (3/4) = (2 4) (3/4) = 2 (4*3/4) = 2 3 = 8.
4. Вычислить 24 (2/3) .
- 24 (2/3) = ((2 3)*3) (2/3) = (2 (2*2/3))*3 (2/3) = 4*3√(3 2)=4*3√9.
5. Вычислить (8/27) (1/3) .
- (8/27) (1/3) = (8 (1/3))/(27 (1/3)) = ((2 3) (1/3))/((3 3) (1/3))= 2/3.
6. Упростить выражение ((a (4/3))*b + a*b (4/3))/(3√a + 3√b)
- ((a (4/3))*b + a*b (4/3))/(3√a + 3√b) = (a*b*(a (1/3) + b (1/3)))/(1/3) + b (1/3)) = a*b.
7. Вычислить (25 (1/5))*(125 (1/5)).
- (25 (1/5))*(125 (1/5)) =(25*125) (1/5) = (5 5) (1/5) = 5.
8. Упростить выражение
- (a (1/3) - a (7/3))/(a (1/3) - a (4/3)) - (a (-1/3) - a (5/3))/(a (2/3) + a (-1/3)).
- (a (1/3) - a (7/3))/(a (1/3) - a (4/3)) - (a (-1/3) - a (5/3))/(a (2/3) + a (-1/3)) =
- = ((a (1/3))*(1-a 2))/((a (1/3))*(1-a)) - ((a (-1/3))*(1-a 2))/ ((a (-1/3))*(1+a)) =
- = 1 +a - (1-a) = 2*a.
Как видите используя эти свойства, можно значительно упростить некоторые выражения, которые содержат степени с дробными показателями.
Арифметическое действие, которое выполняется последним при подсчете значения выражения, является «главным».
То есть, если ты подставишь вместо букв какие-нибудь (любые) числа, и попытаешься вычислить значение выражения, то если последним действием будет умножение - значит, у нас произведение (выражение разложено на множители).
Если последним действием будет сложение или вычитание, это значит, что выражение не разложено на множители (а значит, сокращать нельзя).
Для закрепления реши самостоятельно несколько примеров:
Примеры:
Решения:
1. Надеюсь, ты не бросился сразу же сокращать и? Еще не хватало «сократить» единицы типа такого:
Первым действием должно быть разложение на множители:
4. Сложение и вычитание дробей. Приведение дробей к общему знаменателю.
Сложение и вычитание обычных дробей - операция хорошо знакомая: ищем общий знаменатель, домножаем каждую дробь на недостающий множитель и складываем/вычитаем числители.
Давай вспомним:
Ответы:
1. Знаменатели и - взаимно простые, то есть у них нет общих множителей. Следовательно, НОК этих чисел равен их произведению. Это и будет общий знаменатель:
2. Здесь общий знаменатель равен:
3. Здесь первым делом смешанные дроби превращаем в неправильные, а дальше - по привычной схеме:
Совсем другое дело, если дроби содержат буквы, например:
Начнем с простого:
a) Знаменатели не содержат букв
Здесь все то же, что и с обычными числовыми дробями: находим общий знаменатель, домножаем каждую дробь на недостающий множитель и складываем/вычитаем числители:
теперь в числителе можно приводить подобные, если есть, и раскладывать на множители:
Попробуй сам:
Ответы:
b) Знаменатели содержат буквы
Давай вспомним принцип нахождения общего знаменателя без букв:
· в первую очередь мы определяем общие множители;
· затем выписываем все общие множители по одному разу;
· и домножаем их на все остальные множители, не общие.
Чтобы определить общие множители знаменателей, сперва разложим их на простые множители:
Подчеркнем общие множители:
Теперь выпишем общие множители по одному разу и допишем к ним все необщие (не подчеркнутые) множители:
Это и есть общий знаменатель.
Вернемся к буквам. Знаменатели приводятся по точно такой же схеме:
· раскладываем знаменатели на множители;
· определяем общие (одинаковые) множители;
· выписываем все общие множители по одному разу;
· домножаем их на все остальные множители, не общие.
Итак, по порядку:
1) раскладываем знаменатели на множители:
2) определяем общие (одинаковые) множители:
3) выписываем все общие множители по одному разу и домножаем их на все остальные (неподчеркнутые) множители:
Значит, общий знаменатель здесь. Первую дробь нужно домножить на, вторую - на:
Кстати, есть одна хитрость:
Например: .
Видим в знаменателях одни и те же множители, только все с разными показателями. В общий знаменатель пойдут:
в степени
в степени
в степени
в степени.
Усложним задание:
Как сделать у дробей одинаковый знаменатель?
Давай вспомним основное свойство дроби:
Нигде не сказано, что из числителя и знаменателя дроби можно вычитать (или прибавлять) одно и то же число. Потому что это неверно!
Убедись сам: возьми любую дробь, например, и прибавь к числителю и знаменателю какое-нибудь число, например, . Что поучилось?
Итак, очередное незыблемое правило:
Когда приводишь дроби к общему знаменателю, пользуйся только операцией умножения!
Но на что же надо домножить, чтобы получить?
Вот на и домножай. А домножай на:
Выражения, которые невозможно разложить на множители будем называть «элементарными множителями».
Например, - это элементарный множитель. - тоже. А вот - нет: он раскладывается на множители.
Что скажешь насчет выражения? Оно элементарное?
Нет, поскольку его можно разложить на множители:
(о разложении на множители ты уже читал в теме « »).
Так вот, элементарные множители, на которые ты раскладываешь выражение с буквами - это аналог простых множителей, на которые ты раскладываешь числа. И поступать с ними будем таким же образом.
Видим, что в обоих знаменателях есть множитель. Он пойдет в общий знаменатель в степени (помнишь, почему?).
Множитель - элементарный, и он у них не общий, значит первую дробь на него придется просто домножить:
Еще пример:
Решение:
Предже, чем в панике перемножать эти знаменатели, надо подумать, как их разложить на множители? Оба они представляют :
Отлично! Тогда:
Еще пример:
Решение:
Как обычно, разложим знаменатели на множители. В первом знаменателе просто выносим за скобки; во втором - разность квадратов:
Казалось бы, общих множителей нет. Но если присмотреться, то и так похожи… И правда:
Так и напишем:
То есть получилось так: внутри скобки мы поменяли местами слагаемые, и при этом знак перед дробью поменялся на противоположный. Возьми на заметку, так поступать придется часто.
Теперь приводим к общему знаменателю:
Усвоил? Сейчас проверим.
Задачи для самостоятельного решения:
Ответы:
Тут надо вспомнить еще одну - разность кубов:
Обрати внимание, что в знаменателе второй дроби не формула «квадрат суммы»! Квадрат суммы выглядел бы так: .
А - это так называемый неполный квадрат суммы: второе слагаемое в нем - это произведение первого и последнего, а не удвоенное их произведение. Неполный квадрат суммы - это один из множителей в разложени разности кубов:
Что делать, если дробей аж три штуки?
Да то же самое! В первую очередь сделаем так, чтобы максимальное количество множителей в знаменателях было одинаковым:
Обрати внимание: если поменять знаки внутри одной скобки, знак перед дробью меняется на противоположный. Когда меняем знаки во второй скобке, знак перед дробью снова меняется на противоположный. В результате он (знак перед дробью) не изменился.
В общий знаменатель выписавыем полностью первый знаменатель, а потом дописываем к нему все множители, которые еще не написаны, из второго, а потом из третьего (и так далее, если дробей больше). То есть получается вот так:
Хм… С дробями-то понятно что делать. Но вот как быть с двойкой?
Все просто: ты ведь умеешь складывать дроби? Значит, надо сделать так, чтобы двойка стала дробью! Вспоминаем: дробь - это операция деления (числитель делится на знаменатель, если ты вдруг забыл). И нет ничего проще, чем разделить число на. При этом само число не изменится, но превратится в дробь:
То, что нужно!
5. Умножение и деление дробей.
Ну что же, самое сложное теперь позади. А впереди у нас самое простое, но при этом самое важное:
Порядок действий
Какой порядок действий при подсчете числового выражения? Вспомни, посчитав значение такого выражения:
Посчитал?
Должно получиться.
Итак, напоминаю.
Первым делом вычисляется степень.
Вторым - умножение и деление. Если умножений и делений одновременно несколько, делать их можно в любом порядке.
И напоследок выполняем сложение и вычитание. Опять же, в любом порядке.
Но: выражение в скобках вычисляется вне очереди!
Если несколько скобок умножаются или делятся друг на друга, вычисляем сначала выражение в каждой из скобок, а потом умножаем или дели их.
А если внутри скобок есть еще одни скобки? Ну давай подумаем: внутри скобок написано какое-то выражение. А при вычислении выражения в первую очередь надо делать что? Правильно, вычислять скобки. Ну вот и разобрались: сначала вычисляем внутренние скобки, потом все остальное.
Итак, порядок действий для выражения выше такой (красным выделено текущее дествие, то есть действие, которое выполняю прямо сейчас):
Хорошо, это все просто.
Но это ведь не то же самое, что выражение с буквами?
Нет, это то же самое! Только вместо арифметических действий надо делать алгебраические, то есть действия, описанные в предыдущем разделе: приведение подобных , сложение дробей, сокращение дробей и так далее. Единственным отличием будет действие разложения многочленов на множители (его мы часто применяем при работе с дробями). Чаще всего для разложения на множители нужно применять я или просто выносить общий множитель за скобки.
Обычно наша цель - представить выражение в виде произведения или частного.
Например:
Упростим выражение.
1) Первым упрощаем выражение в скобках. Там у нас разность дробей, а наша цель - представить ее как произведение или частное. Значит, приводим дроби к общему знаменателю и складываем:
Больше это выражение упростить невозможно, все множители здесь - элементарные (ты еще помнишь, что это значит?).
2) Получаем:
Умножение дробей: что может быть проще.
3) Теперь можно и сократить:
Ну вот и все. Ничего сложного, правда?
Еще пример:
Упрости выражение.
Сначала попробуй решить сам, и уж только потом посмотри решение.
Решение:
Перво-наперво определим порядок действий.
Сначала выполним сложение дробей в скобках, получится вместо двух дробей одна.
Потом выполним деление дробей. Ну и результат сложим с последней дробью.
Схематически пронумерую действия:
Теперь покажу весть процесс, подкрашивая текущее действие красным:
1. Если есть подобные, их надо немедленно привести. В какой бы момент у нас ни образовались подобные, их желательно приводить сразу.
2. То же самое касается сокращения дробей: как только появляется возможность сократить, ей надо воспользоваться. Исключение составляют дроби, которые ты складываешь или вычитаешь: если у них сейчас одинаковые знаменатели, то сокращение нужно оставить на потом.
Вот тебе задачи для самостоятельного решения:
И обещанная в самом начале:
Ответы:
Решения (краткие):
Если ты справился хотя бы с первыми тремя примерами, то тему ты, считай, освоил.
Теперь вперед к обучению!
ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ. КРАТКОЕ ИЗЛОЖЕНИЕ И ОСНОВНЫЕ ФОРМУЛЫ
Базовые операции упрощения:
- Приведение подобных : чтобы сложить (привести) подобные слагаемые, надо сложить их коэффициенты и приписать буквенную часть.
- Разложение на множители: вынесение общего множителя за скобки, применение и т.д.
- Сокращение дроби
: числитель и знаменатель дроби можно умножать или делить на одно и то же ненулевое число, от чего величина дроби не изменяется.
1) числитель и знаменатель разложить на множители
2) если в числителе и знаменателе есть общие множители , их можно вычеркнуть.ВАЖНО: сокращать можно только множители!
- Сложение и вычитание дробей:
; - Умножение и деление дробей:
;