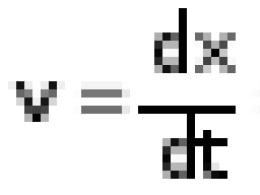Координаты точки пересечения прямой и плоскости - примеры нахождения. Пересечение прямой линии с плоскостью

77*. Найти точку пересечения прямой АВ с плоскостью, заданной треугольником CDE (рис. 75, а).

Решение. Как известно, для нахождения точки пересечения прямой с плоскостью общего положения следует через прямую провести вспомогательную плоскость (R), построить линию пересечения этой плоскости с заданной (1-2) и найти

точку пересечения (К) заданной и построенной прямых. Точка К является искомой точкой пересечения прямой с плоскостью (рис. 75, б). В качестве вспомогательной плоскости обычно используют горизонтально- или фронтально-проецирующую плоскость.

На рис. 75, в через прямую АВ проведена фронтально-проецирующая плоскость R, ее след R ϑ совпадает с а"в". горизонт. след плоскости в данной задаче не нужен и поэтому не показан.

Строим линию пересечения плоскости R и плоскости, заданной треугольником CDE (пример такого построения см. в задаче 67). Построив линию 1-2 (рис. 75, в), находим точку пересечения ее с прямой АВ - точку К (k, k").

Для определения участков прямой АВ, которые будут закрыты треугольником, следует воспользоваться анализом положения точек на скрещивающихся прямых.

Например, точки 1 и 3 находятся на скрещивающихся прямых (соответственно) ED и АВ. Фронтальные проекции этих точек совпадают, т. е. точки 1 и 3 одинаково удалены от пл. Н. Но расстояния их от пл. V различны: точка 3 находится дальше от пл. V, чем точка 1. Поэтому по отношению к пл. V точка 3 закрывает точку 1 (направление взгляда указано стрелкой S). Следовательно, прямая АВ проходит перед треугольником CDE до точки К. Начиная же от точки К влево прямая АВ закрывается треугольником, и поэтому этот участок прямой показан штриховой линией.

Для выявления невидимого участка на горизонт. проекции прямой АВ рассмотрим точки 4 и 5, лежащие соответственно на прямых АВ и CD.

Если смотреть на эти точки по направлению s 1 , мы видим сначала точку 5. Точка 4 закрывается точкой 5. Следовательно, прямая АВ в этом месте закрыта треугольником CDE, и участок ее проекции от точки k до точки 4 должен быть показан штриховой линией. В данном случае точка К оказалась внутри контура треугольника CDE.

При ином взаимном положении пересекающихся элементов возможен случай, когда точка К окажется вне треугольника (рис. 75, г). Это означает, что прямая АВ пересекает плоскость, заданную треугольником CDE, вне контура этого треугольника. АВ становится невидимой за точкой К (влево).

78. Найти точки пересечения прямой АВ с гранями пирамиды (рис. 76). Грани пирамиды следует рассматривать как плоскости, заданные треугольниками.

79. Найти точки пересечения прямой АВ с гранями призмы (рис. 77). Грани призмы следует рассматривать как плоскости, заданные параллельными прямыми.

80*. Найти точки пересечения прямой АВ с плоскостью Р (рис. 78, а).

Решение. Проводим через прямую АВ (рис. 78, бив) фронтально-проецирующую плоскость R (ее след R ϑ совпадает с а"b") и строим линию MN пересечения обеих плоскостей - заданной и проведенной через АВ (построение подобно выполненному в задаче 70). Искомая точка К(k, k") пересечения прямой АВ с плоскостью Р находится в точке пересечения MN с АВ.

В данной задаче видимость участка прямой от точки А до К очевидна; однако в более сложных случаях следует видимый участок прямой определять на основании

анализа положения точек. Например, взяв точку 1 (на прямой АВ) и точку N (на следе Р ϑ). видим, что точка 1 располагается дальше относительно пл. V, чем точка N. Следовательно, прямая АВ до точки К видима. За точкой К прямая показана штриховой линией она невидима. Аналогично определяется видимость на горизонт. проекции.

81. Найти точку пересечения прямой АВ с плоскостью Р (рис. 79).

82*. Найти точку пересечения прямой АВ с плоскостью Р (рис. 80, а).

Решение. Через прямую АВ проводим горизонтально-проецирующую плоскость R (след R h совпадает с ab) и строим линию пересечения плоскостей Р и R,

используя точки М и N пересечения их одноименных следов (рис. 80, б и в). Искомая точка (k", k) находится в точке пересечения МN с АВ. На рис, 80, г точка К построена с помощью пл. W. Так как пл. Р профильно-проецирующая (рис. 80, б).

то профильная проекция k" лежит в точке пересечения следа P ω с а"b". Зная k", строим k" на а"b" и k на аb. Видимые участки прямой АВ определяются так же, как в задачах 77 и 80.

83. Найти точку пересечения прямой АВ с плоскостью Р (рис. 81).

84*. Найти точку пересечения прямой АВ с плоскостью, заданной треугольником CDE (рис. 82, а).

Решение. Через прямую АВ проводим (рис. 82, б и в) пл. R, параллельную пл. W. Она пересекает заданную плоскость по прямой MN (точки m", n", m и n лежат на пересечении следов R ϑ и R h с одноименными проекциями соответствующих сторон

треугольника CDE). Так как прямые АВ и MN профильные, то для нахождения точки (К) их пересечения строим профильные проекции а"b" и m"n". Проекция k" находится на пересечении а"b" и m"m". По k" строим k" на а"b" и k на ab.

85. Найти точку пересечения прямой EF с плоскостью, заданной четырехугольником ABCD (рис. 83).

Построение точки пересечения прямой с проецирующей плоскостью сводится к построению второй проекции точки на эпюре, так как одна проекция точки всегда лежит на следе проецирующей плоскости, потому что все, что находится в проецирующей плоскости, проецируется на один из следов плоскости. На рис. 224,а показано построение точки пересечения прямой EF с фронтально-проецирующей плоскостью треугольника АВС (перпендикулярной плоскости V) На плоскость V треугольник АВС проецируется в отрезок а"с" прямой линии, и точка k" будет также лежать на этой прямой и находиться в точке пересечения е"f" с а"с". Горизонтальную проекцию строят с помощью линии проекционной связи. Види­мость прямой относительно плоскости треугольника ABC определяют по взаимному расположению проекций треугольника ABC и прямой EF на плоскости V. Направление взгляда на рис. 224,а указано стрелкой. Тот участок прямой, фронтальная проекция которого находится выше проекции треугольника, будет видимым. Левее точки k" проекция прямой находится над проекцией треугольника, следовательно, на плоскости H этот участок видимый.

На рис. 224, б прямая EF пересекает горизонтальную плоскость Р. Фронтальная проекция k" точки К - точки пересечения прямой EF с плоскостью Р - будет находиться в точке пересечения проекции е"f" со следом плоскости Рv, так как горизонтальная плоскость является фронтально-проецирующей плоскостью. Горизонтальную проекцию k точки K находят с помощью линии проекционной связи.

Построение линии пересечения двух плоскостей сводится к нахождению двух точек, общих для этих двух плоскостей. Для построения линии пересечения этого достаточно, так как линия пересечения - прямая, а прямая задается двумя точками. При пересечении проецирующей плоскости с плоскостью общего положения одна из проекций линии пересечения совпадает со следом плоскости, находящимся в той плоскости проекций, к которой перпендикулярна проецирующая плоскость. На рис. 225, а фронтальная проекция m"n" линии пересечения MN совпадает со следом Pv фронтально-проецирующей плоскости Р, а на рис. 225,б горизонтальная проекция kl совпадает со следом горизонтально-проецирующей плоскости R. Другие проекции линии пересечения строятся с помощью линий проекционной связи.

Построение точки пересечения прямой с плоскостью общего положения (рис. 226, а) выполняют с помощью вспомогательной проецирующей плоскости R, которую проводят через данную прямую EF. Строят линию пересечения 12 вспомогательной плоскости R с заданной плоскостью треугольника ABC, получают в плоскости R две прямые: EF - заданная прямая и 12 - построенная линия пересечения, которые пересекаются в точке К.

Нахождение проекций точки К показано на рис. 226,б. Построения выполняют в следующей последовательности.

Через прямую EF проводят вспомогательную горизонтально-проецирующую плоскость R. Ее след R H совпадает с горизонтальной проекцией ef прямой EF.

Строят фронтальную проекцию 1"2" линии пересечения 12 плоскости R с заданной плоскостью треугольника ABC с помощью линий проекционной связи, так как горизонтальная проекция линии пересечения известна. Она совпадает с горизонтальным следом R H плоскости R.

Определяют фронтальную проекцию k" искомой точки К, которая находится в пересечении фронтальной проекции данной прямой с проекцией 1"2" линии пересечения. Горизонтальная проекция точки строится с помощью линии проекционной связи.

Видимость прямой относительно плоскости треугольника ABC определяется способом конкурирующих точек. Для определения видимости прямой на фронтальной плоскости проекций (рис. 226,б) сравним координаты Y точек 3 и 4, фронтальные проекции которых совпадают. Координата Y точки 3, лежащей на прямой ВС, меньше координаты Y точки 4, лежащей на прямой EF. Следовательно, точка 4 находится ближе к наблюдателю (направление взгляда указано стрелкой) и проекция прямой изображается на плоскости V видимой. Прямая проходит перед треугольником. Левее точки К" прямая закрыта плоскостью треугольника ABC.

Видимость на горизонтальной плоскости проекций показывают, сравнив координаты Z точек 1 и 5. Так как Z 1 > Z 5 , точка 1 видимая. Следовательно, правее точки 1 (до точки К) прямая EF невидимая.

Для построения линии пересечения двух плоскостей общего положения применяют вспомогательные секущие плоскости. Это показано на рис. 227,а. Одна плоскость задана треугольником ABC, другая - параллельными прямыми EF и MN. Заданные плоскости (рис. 227, а) пересекают третьей вспомогательной плоскостью. Для простоты построений в качестве вспомогательных плоскостей берут горизонтальные или фронтальные плоскости. В данном случае вспомогательная плоскость R является горизонтальной плоскостью. Она пересекает заданные плоскости по прямым линиям 12 и 34, которые в пересечении дают точку К, принадлежащую всем трем плоскостям, а следовательно, и двум заданным, т. е. лежащую на линии пересечения заданных плоскостей. Вторую точку находят с помощью второй вспомогательной плоскости Q. Найденные две точки К и L определяют линию пересечения двух плоскостей.

На рис. 227,б вспомогательная плоскость R задана фронтальным следом. Фронтальные проекции линий пересечения 1"2" и 3"4 плоскости R с заданными плоскостями совпадают с фронтальным следом Rv плоскости R, так как плоскость R перпендикулярна плоскости V, и все, что в ней находится (в том числе и линии пересечения) проецируется на ее фронтальный след Rv. Горизонтальные проекции этих линий построены с помощью линий проекционной связи, проведенных от фронтальных проекций точек 1", 2", 3", 4" до пересечения с горизонтальными проекциями соответствующих прямых в точках 1, 2, 3, 4. Построенные горизонтальные проекции линий пересечения продлевают до пересечения друг с другом в точке k, которая является горизонтальной проекцией точки К, принадлежащей линии пересечения двух плоскостей. Фронтальная проекция этой точки находится на следе Rv.

Для построения второй точки, принадлежащей линии пересечения, проводят вторую вспомогательную плоскость Q. Для удобства построений плоскость Q проведена через точку С параллельно плоскости R. Тогда для построения горизонтальных проекций линий пересечения плоскости Q с плоскостью треугольника АВС и с плоскостью, заданной параллельными прямыми, достаточно найти две точки: с и 5 и провести через них прямые, параллельные ранее построенным проекциям линий пересечения 12 и 34, так как плоскость Q ║ R. Продолжив эти прямые до пересечения друг с другом, получают горизонтальную проекцию l точки L, принадлежащей линии пересечения заданных плоскостей. Фронтальная проекция l" точки L лежит на следе Q v и строится с помощью линии проекционной связи. Соединив одноименные проекции точек К и L, получают проекции искомой линии пересечения.

Если в одной из пересекающихся плоскостей взять прямую и построить точку пересечения этой прямой с другой плоскостью, то эта точка будет принадлежать линии пересечения этих плоскостей, так как она принадлежит обеим заданным плоскостям. Построим таким же образом вторую точку, можно найти линию пересечения двух плоскостей, так как для построения прямой достаточно двух точек. На рис. 228 показано такое построение линии пересечения двух плоскостей, заданных треугольниками.

Для данного построения берут одну из сторон треугольника и строят точку пересечения этой стороны с плоскостью другого треугольника. Если это не удается, берут другую сторону этого же треугольника, затем третью. Если и это не привело к нахождению искомой точки, строят точки пересечения сторон второго треугольника с первым.

На рис. 228 построена точка пересечения прямой EF с плоскостью треугольника ABC. Для этого через прямую EF проводят вспомогательную горизонтально-проецирующую плоскость S и строят фронтальную проекцию 1"2" линии пересечения этой плоскости с плоскостью треугольника АВС. Фронтальная проекция 1"2" линии пересечения, пересекаясь с фронтальной проекцией e"f" прямой EF, дает фронтальную проекцию m" точки пересечения М. Горизонтальную проекцию m точки М находят с помощью линии проекционной связи. Вторая точка, принадлежащая линии пересечения плоскостей заданных треугольников, - точка N - точка пересечения прямой ВС с плоскостью треугольника DEF. Через прямую ВС проводят фронтально-проецирующую плоскость R, и на плоскости H пересечение горизонтальных проекций прямой ВС и линии пересечения 34 дает точку n - горизонтальную проекцию искомой точки. Фронтальная проекция построена с помощью линии проекционной связи. Видимые участки заданных треугольников определяют с помощью конкурирующих точек для каждой плоскости проекций отдельно. Для этого выбирают точку на одной из плоскостей проекций, которая является проекцией двух конкурирующих точек. По вторым проекциям этих точек определяют видимость, сравнивая их координаты.

Например, точки 5 и 6 - точки пересечения горизонтальных проекций bc и de. На фронтальной плоскости проекций проекции этих точек не совпадают. Сравнив их координаты Z, выясняют, что точка 5 закрывает точку 6, так как координата Z 5 , больше координаты Z 6 . Следовательно, левее точки 5 сторона DE невидимая.

Видимость на фронтальной плоскости проекций определяю с помощью конкурирующих точек 4 и 7, принадлежащих отрезкам DE и ВС, сравнивая их координаты Y 4 и Y 7 Так как Y 4 >Y 7 , сторона DE на плоскости V видимая.

Следует отметить, что при построении точки пересечения прямой с плоскостью треугольника точка пересечения может оказаться за пределами плоскости треугольника. В этом случае, соединив полученные точки, принадлежащие линии пересечения, обводят только тот ее участок, который принадлежит обоим треугольникам.

ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ

1. Какие координаты точки определяют ее положение в плоскости V?

2. Что определяют координата Y и координата Z точки?

3. Как располагаются на эпюре проекции отрезка, перпендикулярного плоскости проекций Н? Перпендикулярного плоскости проекций V?

4. Как располагаются на эпюре проекции горизонтали, фронтали?

5. Сформулируйте основное положение о принадлежности точки прямой.

6. Как отличить на эпюре пересекающиеся прямые от скрещивающихся?

7. Какие точки называют конкурирующими?

8. Как определить, какая из двух точек видимая, если их проекции на фронтальной плоскости проекций совпали?

9. Сформулируйте основное положение о параллельности прямой и плоскости.

10. Какой порядок построения точки пересечения прямой с плоскостью общего положения?

11. Какой порядок построении линии пересечения двух плоскостей общего положения?

Линия пересечения двух плоскостей - прямая линия. Рассмотрим сначала частный случай (рис. 3.9), когда одна из пересекающихся плоскостей параллельна горизонтальной плоскости проекций (α π 1 , f 0 α Х). В этом случае линия пересечения а, принадлежащая плоскости α, будет также параллельна плоскости π 1 , (рис. 3.9. а), т. е. будет совпадать с горизонталью пересекающихся плоскостей (а ≡ h).

Если одна из плоскостей параллельна фронтальной плоскости проекций (рис. 3.9. б), то линия пересечения а, принадлежащая этой плоскости, будет параллельна плоскости π 2 и будет совпадать с фронталью пересекающихся плоскостей (а ≡ f).

.

.

Рис. 3.9. Частный случай пересечения плоскости общего положения с плоскостями: а - горизонтального уровня; б - фронтального уровня

Пример построения точки пересечения (К) прямой а (АВ) с плоскостью α (DEF) показан на рис. 3.10. Для этого прямая а заключена в произвольную плоскость β и определена линия пересечения плоскостей α и β.

В рассматриваемом примере прямые АВ и MN принадлежат одной плоскости β и пересекаются в точке К, а так как прямая MN принадлежит заданной плоскости α (DEF), то точка К является и точкой пересечения прямой а (АВ) с плоскостью α. (рис. 3.11).

.

Рис. 3.10. Построение точки пересечения прямой с плоскостью

Для решения подобной задачи на комплексном чертеже необходимо уметь находить точку пересечения прямой общего положения с плоскостью общего положения.

Рассмотрим пример нахождения точки пересечения прямой АВ c плоскостью треугольника DEF представленный на рис. 3.11.

Для нахождения точки пересечения через фронтальную проекцию прямой А 2 В 2 проведена фронтально-проецирующая плоскость β которая пересекла треугольник в точках M и N. На фронтальной плоскости проекций (π 2) эти точки представлены проекциями M 2 , N 2 . Из условия принадлежности прямой плоскости на горизонтальной плоскости проекций (π 1) находятся горизонтальные проекции полученных точек M 1 N 1 . В пересечении горизонтальных проекций прямых А 1 В 1 и M 1 N 1 образуется горизонтальная проекция точки их пересечения (К 1). По линии связи и условиям принадлежности на фронтальной плоскости проекций находится фронтальная проекция точки пересечения (К 2).

.

Рис. 3.11. Пример определения точки пересечения прямой и плоскости

Видимость отрезка АВ относительно треугольника DEF определена методом конкурирующих точек.

На плоскости π 2 рассмотрены две точки NEF и 1АВ. По горизонтальным проекциям этих точек можно установить, что точка N расположена ближе к наблюдателю (Y N >Y 1), чем точка 1 (направление луча зрения параллельно S). Следовательно, прямая АВ, т. е. часть прямой АВ (К 1) закрыта плоскостью DEF на плоскости π 2 (ее проекция К 2 1 2 показана штриховой линии). Аналогично установлена видимость на плоскости π 1 .

Вопросы для самоконтроля

1) В чем заключается сущность метода конкурирующих точек?

2) Какие свойства прямой вы знаете?

3) Каков алгоритм определения точки пересечения прямой и плоскости?

4) Какие задачи называются позиционными?

5) Сформулируйте условия принадлежности прямой плоскости.

Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»

Известно, что прямая пересекает плоскость, если она не принадлежит этой плоскости и не параллельна ей. Следуя приведенному ниже алгоритму, найдем точку пересечения прямой a с плоскостью общего положения α, заданной следами h 0α , f 0α .

Алгоритм

1. Через прямую a проводим вспомогательную фронтально-проецирующую плоскость γ. На рисунке обозначены её следы h 0γ , f 0γ .
2. Строим проекции прямой AB, по которой пересекаются плоскости α и γ. В данной задаче точка B" = h 0α ∩ h 0γ , A"" = f 0α ∩ f 0γ . Точки A" и B"" лежат на оси x, их положение определяется по линиям связи.
3. Прямые a и AB пересекаются в искомой точке K. Её горизонтальная проекция K" = a" ∩ A"B". Фронтальная проекция K"" лежит на прямой a"".

Алгоритм решения останется тем же, если пл. α будет задана параллельными, скрещивающимися прямыми, отсеком фигуры или другими возможными способами .

Видимость прямой a относительно плоскости α. Метод конкурирующих точек

1. Отметим на чертеже фронтально-конкурирующие точки A и С (рис. ниже). Будем считать, что точка A принадлежит пл. α, а С лежит на прямой a. Фронтальные проекции A"" и С"" совпадают, но при этом т. A и С удалены от плоскости проекций П 2 на разное расстояние.
2. Найдем горизонтальные проекции A" и C". Как видно на рисунке, точка C" удалена от плоскости П 2 на большее расстояние, чем т. A", принадлежащая пл. α. Следовательно, участок прямой а"", расположенный левее точки K"", будет видимым. Участок a"" правее K"" является невидимым. Отмечаем его штриховой линией.
3. Отметим на чертеже горизонтально-конкурирующие точки D и E. Будем считать, что точка D принадлежит пл. α, а E лежит на прямой a. Горизонтальные проекции D" и E" совпадают, но при этом т. D и E удалены от плоскости П 1 на разное расстояние.
4. Определим положение фронтальных проекций D"" и E"". Как видно на рисунке, точка D"", находящаяся в пл. α, удалена от плоскости П 1 на большее расстояние, чем т. E"", принадлежащая прямой a. Следовательно, участок а", расположенный правее точки K", будет невидимым. Отмечаем его штриховой линией. Участок a" левее K" является видимым.

Дана прямая: (1) и плоскость: Ax + By + Cz + D = 0 (2).

Найдем координаты точки пересечения прямой и плоскости. Если прямая (1) и плоскость (2) пересекаются, то координаты точки пересечения удовлетворяют уравнениям (1) и (2):

, .

Подставляя найденное значение t в (1), получим координаты точки пересечения.

1) Если Am + Bn + Cp = 0, а Ax 0 + By 0 + Cz 0 + D ≠ 0, то и t не существует, т.е. прямая и плоскость не имеют ни одной общей точки. Они параллельны.

2) Am + Bn + Cp = 0 и Ax 0 + By 0 + Cz 0 + D = 0. В этом случае t может принимать любые значения и , т.е. прямая параллельна плоскости и имеет с ней общую точку, т.е. она лежит в плоскости.

Пример 1. Найти точку пересечения прямой с плоскостью 3x – 3y + 2z – 5 = 0.

3(2t – 1) – 3(4t + 3) + 2·3t – 5 = 0 => -17=0, что невозможно ни при одном t, т.е. прямая и плоскость не пересекаются.

Пример 2. Найти точку пересечения прямой и плоскости: x + 2y – 4z + 1 = 0.

8t + 13 + 2(2t + 1) – 4(3t + 4) + 1 = 0, 0 + 0 = 0. Это верно при любом значении t, т.е. прямая лежит в плоскости.

Пример 3. Найти точку пересечения прямой и плоскости 3x – y + 2z – 5 = 0.

3(5t + 7) – t – 4 + 2(4t + 5) – 5 = 0, 22t + 22 = 0, t = -1, x = 5(-1) + 7 = 2, y = -1 + 4 = 3, z = 4(-1) + 5 = 1, M(2, 3, 1) – точка пересечения прямой и плоскости.

Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости.

Углом между прямой и плоскостью называется острый угол ц между прямой и ее проекцией на плоскость.

Пусть заданы прямая и плоскость:

и .

Пусть прямая пересекает плоскость и образует с ней угол ц (). Тогда б = 90 0 – ц или б = 90 0 + ц – это угол между нормальным вектором плоскости и направляющим вектором прямой . Но . Значит

(3).

а) Если L P, то - условие перпендикулярности прямой и плоскости.

б) Если L||P, то - условие параллельности прямой и плоскости.

в) Если прямая L||P и при этом точка M0(x0, y0, z0) P, то прямая лежит в данной плоскости. Аналитически:

- условия принадлежности прямой и плоскости.

Пример. Дана прямая и точка М 0 (1, 0, –2). Через точку М 0 провести плоскость, перпендикулярную данной прямой. Уравнение искомой плоскости ищем в виде: A(x – 1) + B(y – 0) + C(z + 2) = 0. В данном случая , ,

5(x – 1) – 5y + 5(z + 2) = 0, - x – y + z + 3 = 0.

Пучок плоскостей.

Пучок плоскостей – множество всех плоскостей, проходящих через заданную прямую – ось пучка.

Чтобы задать пучок плоскостей, достаточно задать его ось. Пусть уравнение этой прямой задано в общем виде:

.

Составить уравнение пучка – значит составить уравнение, из которого можно получить при дополнительном условии уравнение любой плоскости пучка, кроме, б.м. одной. Умножим II уравнение на л и сложим с I уравнением:

A 1 x + B 1 y + C 1 z + D 1 + л(A 2 x + B 2 y + C 2 z + D 2) = 0 (1) или

(A 1 + лA 2)x + (B 1 + лB 2)y + (C 1 + лC 2)z + (D 1 + лD 2) = 0 (2).

л – параметр – число, которое может принимать действительные значения. При любом выбранном значении л уравнения (1) и (2) линейные, т.е. это – уравнения некоторой плоскости.

1. Покажем, что эта плоскость проходит через ось пучка L. Возьмем произвольную точку M 0 (x 0 , y 0 , z 0) L. Следовательно, М 0 Р 1 и М 0 Р 2 . Значит:

3x – y + 2z + 9 + 17x + 17z – 51 = 0; 20x – y + 19z – 42 = 0 .

Пример 3 (Э). Составить уравнение плоскости, проходящей через прямую перпендикулярно плоскости x – 2y + z + 5 = 0. ; 3x – 2y + z – 3 + л(x – 2z) = 0; (3 + л)x – 2y + (1 – 2 л)z – 3 = 0; ; ; л = 8; 11x – 2y – 15z – 3 = 0 .